Sommario
Introduzione
La applicazione geometry è una applicazione CLI, cioè a linea di comando che viene eseguito nel terminale a caratteri. Non essendo un ambiente grafico, il terminale a caratteri non può disegnare le figure. Tuttavia, possiamo creare le immagini delle figure geometriche che possono essere visualizzate in un ambiente opportuno come per esempio Windows.
Nella sottocartella javaturor1/projects/design troverete i files sorgente di questo progetto: i nomi dei files sono esattamente li stessi già visti nel capitolo precedente (vedi I files del capitolo) ma il codice è, ovviamente, diverso. Vi è una sola eccezione: il nuovo file sorgente geomart.java che è la applicazione che genera i "quadri" astratti geometrici (vedi La applicazione Geomart).
I formati grafici
Per gestire immagini grafiche, vi sono quattro formati principali:
| Formato | Colori | Note |
|---|---|---|
| JPEG | truecolor | compresso, lossy |
| TIFF | truecolor | compresso, loseless |
| GIF | 256 | compresso, indicizzato |
| PNG | 256 | compresso, indicizzato |
Tutte le implementazioni Java devono garantire di gestire almeno questi quattro formati grafici. I primi due formati sono adatti per immagini di tipo fotografico poichè supportano tutti i colori; vengono chiamati truecolor proprio per questo motivo. In realtà, i due formati truecolor possono gestire "solo" 16.7 milioni di colori (224 colori) ma questo numero è considerato così alto che rappresenta il limite che l'occhio umano può distinguere.
Poichè i nostri disegni hanno pochissimi colori è più adatto uno dei due formati indicizzati che consentono un notevole risparmio di memoria rispetto ai formati truecolor. Il formato GIF però nasconde una insidia: quando è stato introdotto nel 1987 da Compuserve quest'ultima usò il metodo LZW per la compressione dei dati. Tuttavia, il metodo di compressione LZW è brevettato da Unisys la quale pretese il pagamento delle royalties per il suo uso. Benchè il brevetto sia nel frattempo scaduto, la richiesta di royalties da parte di CompuServe ed Unisys portò alla nascita di un formato alternativo, libero da brevetti e molto simile al GIF: il Portable Network Graphics (PNG).
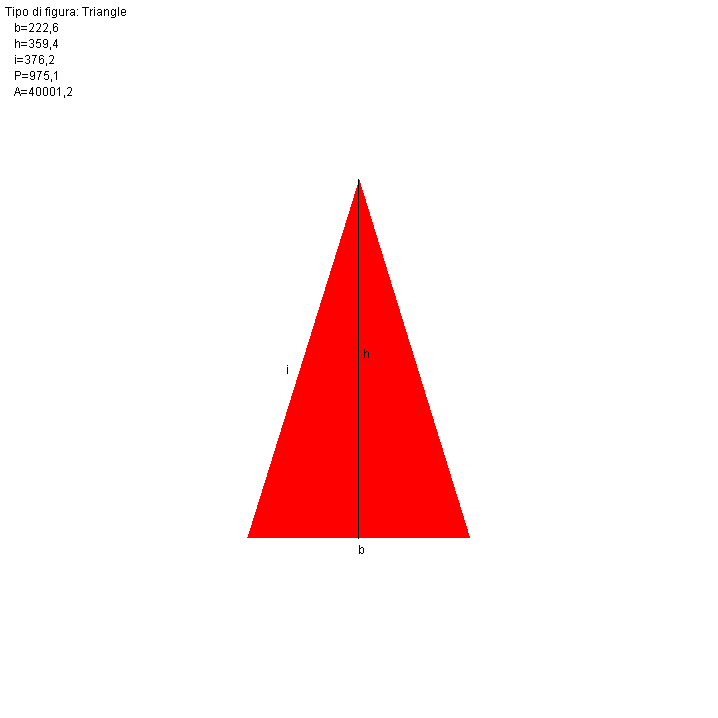
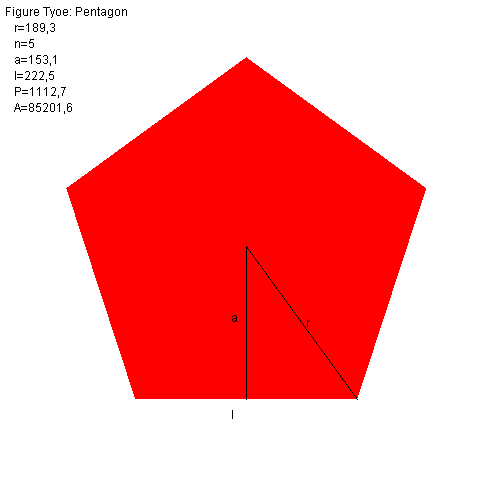
Quindi è il PNG il formato che sceglieremo per implementare il disegno delle figure geometriche gestite dalla applicazione presentata nel capitolo precedente. Il disegno avverrà su di un file su disco che potremmo poi visualizzare usando una delle applicazioni disponibili nel nostro sistema. I disegni PNG che vogliamo ottenere sono simili a questi:
| Triangle | Circle | Square | Pentagon |
|---|---|---|---|
| 
| 
| 
|
La nuova sintassi del comando
Per disegnare le figure geometriche abbiamo bisogno di ulteriori opzioni al comando Geometry. La nuova sintassi sarà la seguente:
Le OPTIONS possono essere:
-h[ITEM]: visualizza help, la stringa ITEM può essere "SHAPE" oppure "COLOR" e visualizza la pagina di aiuto sugli argomenti SHAPE e COLOR-fFILENAME:specifica il nome del file PNG; l'estensione del file ".png", se non indicata, viene aggiunta automaticamente-i:non stampa le informazioni sulla figura nel disegno PNG-cCOLOR:specifica il colore della forma nel disegno-l:non riempire di colore la forma; disegna solo il perimetro-r:non ruotare le figure del disegno PNG, vedi La rotazione dei poligoni regolari-sSIZE:la dimensione del font da usare per le informazioni nel file PNG
L'argomento SHAPE è lo stesso già visto in La sintassi della app Geometry. mentre l'opzione -c permette di specificare, nel suo argomento, un colore per il disegno.
L'opzione color
Specificando l'opzione -cCOLOR è possibile scegliere il colore del disegno della figura PNG. Il colore può essere specificato con un nome di colore tra i seguenti: BLACK, BLUE, CYAN, GRAY, GREEN, MAGENTA, ORANGE, PINK, RED, WHITE, YELLOW.
E' anche possibile specificare il colore come una tripletta di componenti RGB nel range 0 .. 255 separati dal carattere virgola. Esempi:
-cRED specifica il colore rosso -c127,255,212 specifica il colore "aqua marine"
Se non viene specificata l'opzione colore, il default è il colore RED.
I packages della libreria
Prima di addentrarci nei dettagli del disegno è necessaria una panoramica sulle classi che la libreria standard Java mette a disposizone del programmatore per facilitare il lavoro:
BufferedImagerappresenta una immagine grafica in memoria di dimensioni a piacere e che supporta vari formati di coloreColorrappresenta un colore con cui disegnare. Viene costruito con un valore per le tre componenti di colore fondamentali: rosso, verde e blue (RGB)Graphics2Drappresenta il contesto grafico in cui avvengono le operazioni di disegno vero e proprio; il contesto è sempre legato ad uno specifico device (=dispositivo); nel nostro caso il device è la immagine in memoriaFontrappresenta la famiglia, il tipo e la dimensione dei caratteri con cui si disegnano le stringhe nel contesto graficoImageIOuna classe che contiene solo metodi statici usati per scrivere su un file le immagini create nel contesto grafico e per leggere da un file su disco una immagine
Poichè queste classi (ed altre necessarie) non appartengono al package java.lang è necessario importarle esplicitamente in ognuno dei files sorgente:
Il metodo astratto draw
Dobbiamo aggiungere alla classe base astratta un metodo da richiamare dal main se l'utente vuole il disegno della figura:
Il metodo è, ovviamente, astratto dal momento che la classe base nulla sa di cosa disegnare: potrebbe essere qualsiasi figura geometrica tra quelle gestite. Gli argomenti al metodo sono i seguenti:
flags:contiene le opzioni booleane relative al disegno vedi I flags di disegno)coloril colore della figura geometricafontil font da usare nel disegno delle stringhe delle informazioni; questo argomento può essere null nel qual caso di usa il font di default
il metodo restituisce un oggetto di classe BufferedImage che rappresenta una immagine in memoria; essa può essere disegnata su un device fisico, come lo schermo, su una altra immagine in memoria oppure scritta su di un file su disco in uno dei formati previsti, che è proprio l'operazione che andremo ad implementare.
I flags di disegno
Normalmente, il metodo draw disegna la figura geometrica riempiendola del colore selezionato, con le informazioni scritte nell'angolo superiore sinistro e con la rotazione dei poligoni regolari (quello della rotazione è un problema che affronteremo in La rotazione dei poligoni regolari).
E' possibile per l'utente specificare alcune opzioni per modificare questo comportamento:
- l'opzione
-iviene usata per sopprimere il disegno delle informazioni - l'opzione
-lviene usata per disegnare solo il perimetro della figura - l'opzione
-rviene usata per sopprimere la rotazione
Per tenere traccia di queste opzioni sono sufficenti tre variabili di tipo boolean:
Queste tre opzioni devono essere passate come argomenti al metodo astratto draw in modo che esso possa disegnare la figura nel modo desiderato dal utente. Il metodo draw quindi dovrebbe essere dichiarato così:
Tuttavia, se in futuro dovessimo aggiungere una opzione di disegno di tipo booleano dovremmo aggiungere un parametro al metodo draw e questo romperebbe la compatibilità con tutto il software scritto fino a questo momento usando le nostre classi di gestione delle figure geometriche (dubito che ciò accada ma ... mai dire mai).
Senza alcun dubbio, una soluzione c'è ed è la più facile: il nuovo metodo che accetta una quarta opzione di disegno potrebbe chiamarsi in modo diverso, per esempio draw2, ed il software già scritto (per ora la sola applicazione Geometry) funzionerebbe ancora. Ma c'è una soluzione molto più elegante.
Una variabile di tipo boolean ha solo due stati: vero oppure falso e quindi è sufficiente un solo bit per memorizzarla ( "0" oppure "1") e poichè in un intero ci sono 32 bits (vedi I tipi primitivi), possiamo racchiudere tutte le tre opzioni di cui sopra in una unica variabile di tipo intero con il vantaggio che possiamo implementare una quarta (e quinta, e sesta e...) opzione senza dover modificare la dichiarazione del metodo draw che continuerà ad accetttare un intero finchè non arriveremo a superare le 32 opzioni.
In gergo informatico una variabile booleana si chiama flag (=bandiera) e la variabile intera che ne contiene due o più viene comunemente chiamata flags.
L'accesso ai singoli bits di una variabile si ottiene attraverso gli Operatori di bitwise specificando opportunamente delle costanti che li indirizzano sapendo che il primo bit meno significativo vale 1, il secondo bit vale 2, il terzo vale 4 e così via secondo le potenze del 2.
Definiremo quindi nella classe Figure tre costanti mnemoniche che indirizzano i tre bit meno significativi della variabile flags:
Per impostare il bit a UNO useremo l'operatore di bitwise OR (|) eseguito tra la variabile flags, inizializzata a ZERO, e la costante mnemonica. Questa operazione viene eseguita nel metodo parseCmdline della classe Geometry:
Se vengono specificate tutte e tre le opzioni, il valore finale della variabile flags sarà 4+2+1=7, in binario vale 111.
Come si verifica se uno dei bits è impostato o meno? Con l'operatore di bitwise AND (&) eseguito tra la variabile flags e la costante mnemonica relativa. Esempio:
L'espressione suesposta darà risultato ZERO se il bit relativo a NO_INFO non è impostato. Un valore diverso da ZERO significa che il bit è impostato.
Il metodo concreto drawInfo
Come già avvenuto per la versione precedente della applicazione nella quale il metodo prinInfo era un metodo concreto (vedi I metodi concreti (non astratti)) anche il metodo drawInfo è un metodo concreto. Infatti questo metodo disegna le informazioni sulla figura geometrica ottenendo le stringhe delle informazioni variabili dal metodo astratto getInfo, che abbiamo già scritto.
Questo metodo è molto simile a printInfo: disegna le informazioni comuni a tutte le figure geometriche come il tipo di figura, il perimetro e l'area e itera sulla array di stringhe restituite dal metodo astratto getInfo per disegnare le informazioni variabili, quelle che dipendono dal tipo di figura.
Un breve commento meritano le istruzioni che appaiono all'inizio del metodo drawInfo. Mentre nel terminale a caratteri usiamo il metodo println per stampare a video una qualsiasi stringa ed andare automaticamente a capo-riga, in un contesto grafico il metodo println non esiste e non esiste nemmeno il concetto di a capo riga.
Il contesto grafico si basa sulle coordinate grafiche che, come vedremo nella sezione seguente, identificano un punto nel contesto dove si può disegnare. Il metodo per scrivere una stringa in un contesto grafico è il seguente:
Come primo parametro si deve fornire la stringa da disegnare mentre nei due parametri successivi si devono specificare le coordinate X,Y della superficie di disegno. Una volta disegnata la stringa non esiste alcun ritorno-a-capo-riga semplicemente perchè nella superficie di disegno non esiste alcuna riga.
Per "andare a capo-riga" si deve semplicemente calcolare una nuova coordinata Y dove disegnare la stringa successiva e questo calcolo è piuttosto facile da fare: basta aggiungere alla cooridnata Y attuale la altezza della stringa in pixels.
Ovviamente, la altezza della stringa disegnata nel contesto grafico dipende dal font usato per la scrittura che può essere impostato nel contesto grafico per mezzo del metodo setFont. Se non viene impostato un font specifico ogni contesto grafico viene creato con un font di default.
Ogni font selezionato nel contesto grafico possiede delle caratteristiche specifiche tra cui la altezza in pixels. Queste caratteristiche vengono chiamate metrics (=metriche) e possono essere ottenute con il metodo getFontMetrics del contesto grafico. Una volta ottenute le metriche, possiamo ottenere la altezza in pixels del font usato col metodo getHeight. Quindi:
Usiamo pertanto il valore di lineHeight per calcolare la nuova coordinata Y dove scrivere la stringa successiva simulando così una specie di "ritorno-a-capo".
Il disegno del rettangolo
Questo è il disegno più semplice da fare poichè le primitive grafiche sono in gran parte basate sui rettangoli. Per disegnare un rettangolo si usano i due metodi drawRect e fillRect della classe Graphics una classe base astratta da cui deriva Graphics2D.
La differenza tra i due metodi è che il primo disegna solo il perimetro del rettangolo mentre il secondo lo riempie col colore selezionato. I due metodi accettano entrambi quattro parametri:
xla coordinata X dell'angolo in alto a sinistra del rettangoloyla coordinata Y dell'angolo in alto a sinistra del rettangolowidthla larghezza del rettangoloheightla altezza del rettangolo
Lo schema di coordinate del contesto grafico parte dall'angolo superiore sinistro e si espande a destra per le coordinate X ed in basso per le coordinate Y:
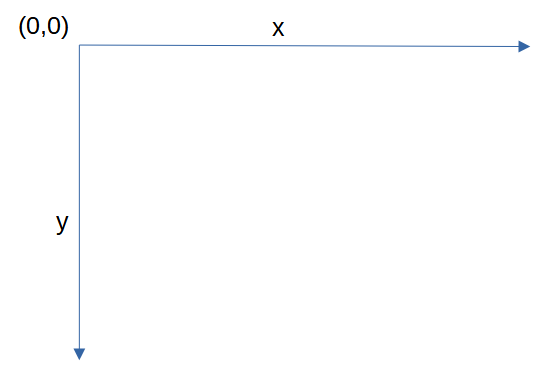
Per disegnare il rettangolo dobbiamo pertanto determinare:
- la dimensione della superficie di disegno
- la coordinata X,Y dell'angolo superiore sinistro in modo tale che il disegno sia centrato nella superficie
L'implementazione del metodo draw per il rettangolo comincia con il primo punto; stabiliamo che le dimensioni della superficie siano il doppio della misura più grande tra la base e l'altezza:
Per quanto riguarda il secondo punto, calcoliamo la coordinata X,Y del angolo superiore sinistro dividendo a meta la differenza tra le due dimensioni della superficie e la base e l'altezza del rettangolo:
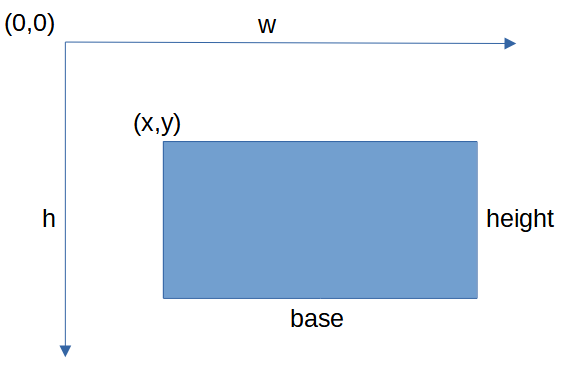
Il codice è piuttosto semplice:
Creiamo quindi l'immagine in memoria con le dimensioni w e h calcolate in precedenza istanziando la classe BufferedImage il cui costruttore accetta, oltre ai due argomenti widht ed height un terzo argomento: il tipo di immagine da creare.
Vi sono molti tipi di immagine che si possono creare ma quello più usato e compatibile con tutti i contesti grafici è il TYPE_INT_ARGB che usa un intero a 32 bits per i tre componenti fondamentali di colore (8-bits ciascuno); gli 8 bits rimanenti vengono riservati al canale alpha, cioè all'attributo di trasparenza. Dopo aver istanziato l'immagine ne otteniamo il contesto grafico per potervi disegnare sopra e riempiamo la immagine con uno sfondo bianco:
Ora che abbiamo calcolato tutti i parametri non dobbiamo fare altro che disegnare effettivamente il rettangolo:
- selezioniamo il colore del disegno nel contesto grafico, stabilito dal parametro
colordel metodo che stiamo scrivendo - se il flag
NO_FILLè impostato useremo la primitivadrawRect; in caso contrario useremo lafillRect
Se l'utente vuole le informazioni sulla figura geometrica stampate nel disegno, selezioneremo nel contesto grafico il colore ed il font da usare per esse e richiameremo il metodo drawInfo:
Infine, liberiamo il contesto grafico e restituiamo l'immagine al chiamante:
Benchè il metodo dispose non sia assolutamente necessario dal momento che la JVM si occupa automaticamente del rilascio delle risorse attraverso il garbage collector, è buona norma accelerare questo processo perchè i contesti grafici sono notoriamente avidi di risorse; prima riusciamo a liberare le risorse allocate per il contesto, meglio è. Se volete saperne di più, leggete la documentazione ufficiale.
Il disegno della ellisse
Probabilmente ricorderete (o forse no) che quando abbiamo scritto la classe Circle ci siamo chiesti a che scopo derivarla da Ellipse dal momento che nessuno dei metodi nè dei membri dati della classe base è stato riutilizzato nella derivata (vedi La classe Circle).
La risposta è questa: il metodo sovrascritto draw col quale disegnamo la ellissi può essere usato anche per disegnare un cerchio.
Infatti, la primitiva grafica per il disegno di una ellisse e di un cerchio è sempre la stessa: drawOval la quale disegna un ovale, quindi una ellisse. Come già visto per il rettangolo, il metodo drawOval disegna solo il perimetro della ellissi, mentre il metodo fillOval la riempie del colore selezionato nel contesto.
Gli argomenti da fornire a questi due metodi sono gli stessi già visti per disegnare un rettangolo: le cooridnate X e Y dell'angolo in alto a sinistra e la larghezza ed altezza del rettangolo che racchiude la ellisssi; in questo senso, la dimensione dell'asse orizzontale della ellissi coincide con la larghezza del rettangolo mentre la misura dell'asse verticale della ellisse coincide con l'altezza del rettangolo:
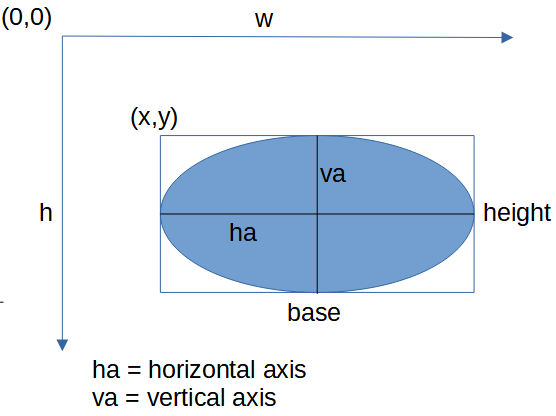
Quindi il codice per disegnare una ellisse è praticamente lo stesso di quello usato per disegnare un rettangolo, salvo richiamare la primitiva grafica drawOval o fillOval in luogo della drawRect o fillRect. Per quanto riguarda le informazioni da disegnare, la ellisse si discosta leggermente dal rettangolo poichè vengono disegnate le linee dei due assi (orizzontale e verticale):
Ma il cerchio? La classe Circle eredita il metodo draw da Ellipse e poichè un cerchio non è altro che una ellisse con i due assi (orizzontale e verticale) coincidenti, ne consegue che l'ovale disegnato dal metodo drawOval rappresenta, in effetti, un cerchio.
Una differenza rispetto alla ellisse nel cerchio esiste: benchè il metodo draw ereditato dalla classe base funziona, nel cerchio non dobbiamo disegnare i due assi orizzontale e verticale bensì il suo raggio.
Per questo motivo sovrascriveremo il metodo drawHorizAxis in modo che esso disegni il raggio ed il metodo drawVertAxis in modo che non esegua nulla dal momento che non è necessario disegnare l'asse verticale nel cerchio.
Il disegno del triangolo
A differenza di rettangoli ed ellissi, non esistono primitive grafiche per disegnare un triangolo ma possiamo usare per questo scopo una primitiva che consente di disegnare qualsiasi poligono composto da tre o più lati. La primitiva in argomento è la drawPolygon (e la sua controparte fillPolygon) che accetta come argomento un oggetto di classe Polygon il quale a sua volta descrive un poligono come l'insieme delle linee che collegano tre o più punti sul piano del contesto grafico.
Schematicamente, un triangolo isoscele viene rappresentato dai tre punti A, B e C dei quali dobbiamo calcolare le coordinate X,Y:
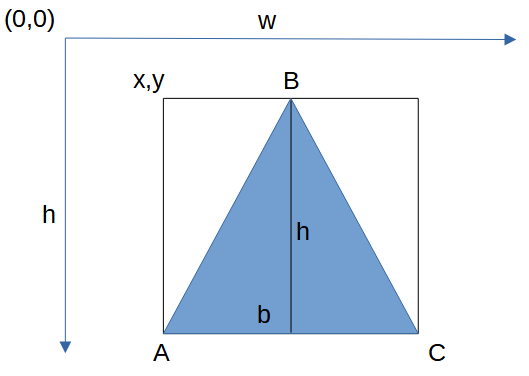
Possiamo anche notare che il triangolo è inserito in un ipotetico rettangolo il cui angolo in alto a sinistra ha coordinate x,y che noi calcoliamo per centrare il disegno nel piano del contesto grafico, come d'altronde già fatto per tutte le altre figure.
Dopo aver calcolato le coordinate del angolo in alto a sinistra, è facile calcolare le coordinate dei tre punti A,B e C:
A(x) = x ; A(y) = y + height B(x) = x+base/2 ; B(y) = y C(x) = x+base ; C(y) = y + height
Per tenere traccia dei tre punti creiamo una array di oggetti Point, una classe che fà parte della libreria standard di Java. Per costruire un oggetto Point è necessario fornire al suo costruttore due interi: il primo è la coordinata X ed il secondo è la coordinata Y:
Poichè un oggetto Polygon è un insieme di coordinate di punti nel piano del contesto grafico costruiamo l'oggetto Polygon con il suo costruttore di default, cioè vuoto, e poi iteriamo sulla array di punti aggiungendo ogni punto al poligono.
Successivamente, selezioniamo il colore e richiamiamo il metodo drawPolygon per disegnare il triangolo:
Forse sarete rimasti sorpresi dal costrutto usato per istanziare un oggetto di classe Polygon che fa parte della libreria standard di Java:
Non sarebbe stato meglio importare la classe dal suo package come abbiamo fatto per tutte le altre classi della libreria standard di Java?
Non sarebbe stato possibile poichè l'importazione della classe Polygon della libreria sarebbe andata in conflitto con la classe Polygon scritta da noi e presentata in Il disegno del poligono regolare. Daltronde non possiamo nemmeno istanziare la classe Polygon della libreria usandone il semplice nome poichè in quel caso avremmo avuto una istanza della nostra classe e non di quella che intendevamo usare.
La soluzione a questo conflitto è quella di usare il cosidetto fully qualified name (=il nome qualificato per intero) che consiste nel nome della classe preceduto dal nome del package che la contiene. Questa possibilità è aperta a qualsiasi classe e non solo alle eventuali classi in conflitto. Per esempio, non sarebbe necessario importare la classe java.awt.Graphics2D se nel nostro sorgente ci riferissimo ad essa in questo modo:
Il restante codice del metodo draw per la classe Triangle è molto simile a quello degli altri già commentati.
Per la classe EquiTriangle, invece, non viene nemmeno implementato il metodo draw dal momento che quello ereditato dalla sua classe base funziona allo scopo. Saranno invece sovrascritti i metodi:
drawBaseche disegna il lato del triangolodrawHypoche non esegue alcuna operazione dal momento che la ipotenusa dei due triangoli rettangoli è uguale al lato del triangolo
Il disegno del poligono regolare
Il disegno del poligono regolare si basa sullo stesso principio del disegno del triangolo: è necessario e sufficente determinare le coordinate dei punti che congiungono le linee del poligono: per esempio, in un esagono i punti sono sei quindi avremo una array di sei coordinate Point.
Il metodo che descrivo si basa sul algoritmo presentato da Paolo Liberatore (Associate Professor, Department of Computer and System Sciences (DIS), University of Rome "La Sapienza") e pubblicato in questo articolo nel quale viene presentata una applet Java che disegna un qualsiasi poligono regolare.
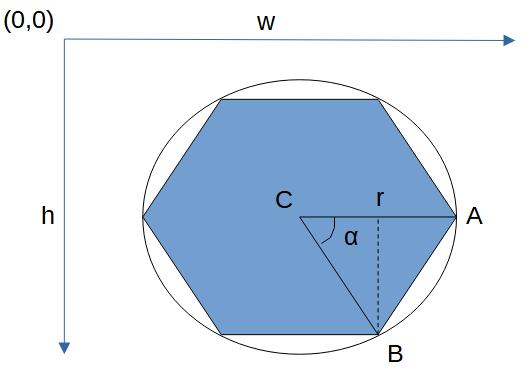
Per centrare il disegno nel piano del contesto grafico calcoliamo le coordinate del centro del cerchio circoscritto al poligono regolare; identifichiamo questo punto con la lettera "C":
Possiamo notare dal disegno che le coordinate del punto A sono facili da calcolare poichè:
A(x) = xcentro + radius; A(y) = ycentro;
Per calcolare le coordinate del punto B dobbiamo aggiungere alle coordinate del centro del cerchio:
- per la coordinata X: il coseno dell'angolo alfa moltiplicato per il raggio
- per la coordinata Y: il seno dell'angolo alfa moltiplicato per il raggio
Allo stesso modo, per tutti gli altri punti, tenendo presente che l'angolo dei vari punti, partendo dal punto ZERO, è dato dalla formula: 360° / n dove n è il numero dei lati del poligono.. Per disegnare la sola figura del poligono regolare è stato definito un metodo specifico che viene richiamato dal metodo draw: questo metodo è stato chiamato drawFigure e prende come argomenti:
gil contesto grafico in cui disegnarenil numero di lati del poligonocoloril colore selezionato per il disegnoxcenterla coordinata X del centro del cerchio circoscrittoycenterla coordinata Y del centro del cerchio circoscrittorotationl'angolo di rotazione della figura (ne parliamo proprio nella sezione successiva)flagsi flags di disegno dei quali solo il NO_FILL viene preso in considerazione
Infine, richiamiamo il metodo drawPolygon per disegnare il poligono regolare dopo aver selezionato il colore desiderato dall'utente.
La rotazione dei poligoni regolari
Il metodo drawFigure presentato dal professor Paolo Liberatore nel suo articolo Poligoni regolari soffre di un piccolo inconveniente: le figure disegnate sono, come dire, storte nel senso che non sono orientate come noi ci aspettiamo. Questi sono alcuni esempi di output:
| Triangle | Square | Pentagon |
|---|---|---|

| 
| 
|
Questo output piuttosto curioso è dovuto al fatto che il punto A cioè il primo punto calcolato col metodo del seno e coseno è sempre a coordinate:
A(x) = xcentro + radius A(y) = ycentro
dal momento che:
sin(0) = 0 cos(0) = 1
Infatti, la variabile i del ciclo for è inizializzata a ZERO ed è pertanto ovvio che la ampiezza del primo angolo sarà sempre pari a ZERO.
La soluzione a questo inconveniente è quella di ruotare la figura di un certo numero di gradi che, per il quadrato, è di 45°.

Il grado di rotazione dipende dal tipo di poligono regolare e viene aggiunta già in fase di calcolo delle coordinate dei vari punti del poligono:
Purtroppo, non sono riuscito a stabilire una qualche relazione tra il numero di lati del poligono e il grado di rotazione necessaria ad ottenere una figura accettabile. Ho usato un programma di image editing per calcolare a mano tutte le rotazioni necessarie per i poligoni fino al icosagono (20 lati) mentre per quelle con più di 20 lati non ci sarà rotazione.
Il seguente metodo restituisce il grado di rotazione in radianti per tutti i poligoni; per quelli con un numero di lati maggiore di 20 restituisce ZERO.
La applicazione Geomart
Questo programmino è molto semplice. Il nome è la contrazione di geometric art poichè disegna dei quadri di arte geometrica salvando il disegno in un file PNG. L'unico argomento obbligatorio sulla command line è il nome del file dove salvare il disegno.
Il programma crea un quadro di 800 x 600 pixels disegnando 40 poligoni regolari di dimensione casuale con un numero di lati casuale compreso tra 3 e 6. Anche i colori dei poligoni sono scelti a caso dal programma in base ad un valore minimo (20) e ad un valore massimo (255) per i tre componenti fondamentali.
Quello che segue è un esempio:

Il programma accetta due argomenti aggiuntivi alla command-line: la larghezza e la altezza del quadro, espressi in pixels. Inoltre possono essere specificate numerose opzioni per personalizzare il risultato finale:
- le opzioni
-r,g,b controllano il valore minimo dei tre colori fondamentali; di default esso è impostato a 20 ma se si specifica un valore più alto, diciamo 220, si avrà un disegno con un colore dominante. Per esempio, l'opzione-r240produrrà un quadro tendente al rosso - le opzioni
-R,G,B controllano il valore massimo dei tre colori fondamentali; di default esso è impostato a 255 ma se si specifica un valore più basso si otterrà un disegno che, tendenzialmente, mancherà di quel colore - la opzione
-nspecifica il numeri di poligoni da disegnre; il default è 40 - le opzioni
-l,L specificano rispettivamente il numero minimo e massimo di lati del poligono; il default è 3 e 6 - la opzione
-aspecifica il moltiplicatore per la dimensione del poligoni (è la misura del raggio del cerchio circoscritto). Questa misura è determinata casualmente ed è compresa tra 10 e il risultato diwidth/n*adoveaè il moltiplicatore. Più alto è questo numero e più grandi saranno i poligoni. Il default è 7
Le interfacce
Abbiamo imparato che derivando classi specializzate da una unica classe base che fà da capostipite possiamo istanziare un oggetto di qualsiasi classe derivata mantenendo il reference della variabile di tipo classe base e mediante riferimento richiamare qualsiasi metodo definito nella classe base e sovrascritto nelle derivate: grazie al meccanismo del polimorfismo il metodo effettivo richiamato è quello della derivata e non della classe base.
Abbiamo anche imparato che i metodi astratti della classe base devono essere OBBLIGATORIAMENTE sovrascritti in TUTTE le classi derivate a meno che esse non siano a loro volta classi base astratte. Infine, abbiamo imparato che è possibile verificare che un metodo di una derivata che noi intendiamo come sovrascrittura del omonimo metodo di una classe base mediante l'uso della annotazione @Override.
La classe base astratta Figure in effetti può disegnare una moltitudine di figure geometriche piane grazie al metodo astratto draw che accetta diversi parametri.
Tuttavia, la classe Figure è limitata al disegno di figure geometriche ma ci possono essere moltri altri oggetti che si possono disegnare: animali, edifici, montagne, piante, pesci etc. Si potrebbe quindi estendere l'albero genealogico prevedendo molti altri genitori fino ad arrivare ad un oggetto che li raggruppa tutti. Ma questa soluzione non è praticabile: l'albero diverrebbe estremamente complesso.
Il linguaggio Java risolve questo problema in modo estremamente elegante con il concetto delle interfacce. Una interfaccia altro non è che un elenco di metodi senza corpo al pari dei metodi astratti: una qualsiasi classe che implementi una interfaccia è obbligata ad implementarne tutti i metodi.
Non solo: una interfaccia definisce un nuovo tipo di dato ed esso può essere usato per riferirsi a qualunque oggetto la implementi. Possiamo pertanto chiudere il nostro albero genealogico con il capostipite Figure (ovviamente possiamo definire molte altre derivate, specializzate nel gestire figure geometriche) e definire una interfaccia Drawable (=disegnabile) che dichiara un solo metodo astratto:
La interfaccia viene definita con la parola chiave interface seguita dal identificativo della interfaccia e dal suo corpo, racchiuso tra una coppia di parentesi graffe (aperta e chiusa). Nel corpo della interfaccia si possono definire:
- membri dati costanti; non è possibile definire dati di istanza poichè una interfaccia non è un oggetto e non è istanziabile
- metodi astratti che devono essere definiti nelle classi che intendono implementare la interfaccia; questi metodi non hanno corpo e terminano con il punto-e-virgola
- metodi statici che possono essere richiamati senza istanziare la interfaccia: questi metodi hanno, ovviamente, un corpo
- i dati ed i metodi sia statici che astratti hanno come attributo di accesso di default
publicquindi questa parola chiave può essere omessa
La classe che implementa la interfaccia deve essere dichiarata usando la parola chiave implements seguita dal nome della interfaccia che si intende implementare:
Poichè la classe Figure implementa la interfaccia Drawable, non è più necessaria la dichiarazione del metodo astratto draw nel corpo della classe Figure: il metodo draw diventa automaticamente un metodo astratto della classe base Figure.
In futuro, quando la nostra applicazione gestirà anche gli animali, possiamo definire una classe Dog che implementi l'interfaccia Drawable. Non avremmp bisogno di un albero genealogico con un capostipite in comune tra il rettangolo ed il cane per riferirsi ad un oggetto di queste due classi e disegnarne la figura:
Mentre una qualsiasi classe può derivare da una ed una sola classe base, non c'è limite al numero di interfaccie che la classe può implementare. Per questo motivo in Java è prassi comune definire molte interfacce ed è altrettanto comune che una classe implementi due o più interfacce.
La documentazione completa in formato javadoc di questo progetto è disponibile al seguente link: Il progetto GeomArt
Argomento precedente - Argomento successivo - Indice Generale
Generato da